Comparative Effectiveness HAP 823

Lecture: Preliminaries for Causal Networks  

 

Assigned Reading

  1. Session Overview
  2. Network Concept 
  3. Student teachers

Assignment

Include in the first page a summary page.  In the summary page write statements comparing your work to answers given or videos.  For example, "I got the same answers as the Teach One video for question 1." 

For these assignment you can use any statistical package, including R, SAS, and SPSS, Python. R packages and BNLearn are also used often.  OpenBUGS and Gibbs Sampler, Stan, OpenMarkov, and Direct Graphical Model are also open source software.  Netica is free for networks less than 15 nodes.

Question 1: This problem is based on example 1.2.1 in the Causal Inferences in Statistics book.  An AI system provided advice on antidepressants based on patient's medical history.  The advice was provided to 700 clinicians at point of care, 350 chose to follow the advice.  Table below shows the number of patients of the clinicians recovering from depression. 

  1. Is the AI system effective for men (i.e. probability effective AI given the person is male)?
  2. Is the AI system effective for women (i.e., probability of effective AI given the person is female)?
  3. Is the AI system effective across the population, if we do not know the gender of the person (i.e. probability of effective AI)?

Number of Patients Recovering
  Advice Followed Advice Not Followed
Men 81 (n=87) 234 (n=270)
Women 192 (n=263) 55 (n=80)
Total  273 (n=350) 289 (350)

Resources for Addressing Question 1:

Question 2: Calculate the following probabilities using the data in the following Table

  1. Probability of being 18 to 29 years old
  2. Probability of being 30 to 40 years old given that you are at least 29 years old
  3. Expected value of age

Age Group # of voters
18-29 20,539
30-44 30,756
45-64 52,013
65+ 29,641

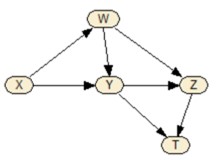
Question 3: Using the following graph, answer the following questions:

  1. Name variables that temporally precede Z.  Use the direction of the arc to set precedence.
  2. Name variables that are not correlated with Z.  Note that in a network, all connected variables are correlated.
  3. Name all of the parents of Z.  Parents precede Z and directly affect Z.
  4. Name all of the ancestors of Z.  Ancestors precede Z but indirectly affect Z through other nodes.
  5. Name all of the children of W.  This is all nodes in which W is a parent of the node. Children follow W and are directly affected by W.
  6. Name all of the descendants of W.  Descendants follow W but indirectly are affected.
  7. Identify all simple paths between X and T, where no node appears more than once. 
  8. Draw all direct paths between X and T.  This includes all arcs where X is start and T is end of the arc.
  9. What is the definition of a directed a-cyclical graph (DAG), and is this graph a DAG?
  10. What is the common cause of Y and Z? Common cause is a parent shared between Y and Z.

xyzwt graph

Question 4: Draw networks based on the following independence assumptions.  When directed networks are possible, give formulas for predicting the last variable in the networks from marginal and pair-wise conditional probabilities.  Keep in mind that absence of independence assumption implies dependence. In the following, the function I(X,Y) indicates that X is independent of Y.  The function I({X,Y}|Z) implies that the joint variable X and Y are independent of Z. This implies that each variable is independent of Z.  If each variable is independent of Z, this is not sufficient to say the joint distribution of X and Y are independent of Z. 

Resources for Question 4:

Nodes in Network Assumption
X, Y, Z I(X,Y)
X, Y, Z I(X,Y), Not I(X,Y|Z)
X, Y, Z I(X,Y), I(X,Y|Z), Y measured last
X, Y, Z, W I(X,Y), I(X,Y|Z), I({X,Y},W|Z), W measured last
X, Y, Z, W II(X,Y), I(Z,W), and X measured before Z and Y measured before W

Optional Question 5: This problem comes from study question 1.3.2 in Causal Inference in Statistics.  Using the proportion of male and females achieving a given level of education, calculate the following probabilities:

  1. Estimate p(High School)
  2. Estimate p(High School OR Female)
  3. Estimate p(High School | Female)
  4. Estimate p(Female| High School)

Education Male  Female
Never Finished High School 112 136
High School 231 189
College 595 763
Graduate School 242 172

More

For additional information (not part of the required reading), please see the following links:

  1. Introduction to causal inference Read 1► Read 2► Video► Slides►
  2. Meta analysis through Bayesian networks Read►
  3. Introduction to Bayesian networks Read►
  4. Learning Bayesian Networks Read►
  5. Selection of Judea Pearl's articles PubMed►
  6. Applications of Bayesian networks in healthcare PubMed►
  7. Bayesian networks in neuroscience Read►
  8. Cost analysis using Bayesian networks Read►
  9. Bayesian network classifiers Read►  

This page is part of the course on Comparative Effectiveness by Farrokh Alemi, Ph.D. Course Home► Email►