Supplement to Chapter on Causal Neworks

Presentations

Assignment

For this assignment you can use any statistical package, including R, SAS, and SPSS.  Your instructor is familiar with Netica and BayesiaLab.  R packages are also used often.  OpenBUGS and Gibbs Sampler, Stan, OpenMarkov, and Direct Graphical Model are open source software.  Netica is free for networks less than 15 nodes. A more complete list is available in Wikipedia under "Bayesian Networks."  OpenBUGS► Stan► Direct Graphical Models► OpenMarkov► Graphical Models Toolkit► PyMC► Genie Smile► SamIam► Bayes Server► AIspace► BayesiaLab► Hugin► AgenaRisk► dVelox► System Modeler► UnBBayes► Uninet► Tetrad► Dezide► Netica►

Work on this assignment can be done in group's of two students but you cannot work with a student that you have previously teamed up with.

Question 1: Draw networks based on the following independence assumptions.  When directed networks are possible, give formulas for predicting the last variable in the networks from marginal and pair-wise conditional probabilities.  Keep in mind that absence of independence assumption implies dependence. Review►

Redo this assignment assuming that W, X, Y, Z occur in order, meaning W before X, X before Y, and Y before Z.  How have your networks changed?  Wang's Video►

Question 2: Construct a Bayesian probability network model that would predict success with citalopram. A network model will include variables, and mediators of the effect of variables, on response to citalopram.   Include at least 5 variables in your model.  Remission or relapse should be considered an end node.  Variables that cannot be altered (e.g. year of birth or family history) should be considered root nodes.  All other  variables, e.g. diagnoses, could be either root or intermediary nodes. The structure of the network model could be based on expert's opinion, analysis of conditional independence, and your own analysis of association among the variables.  The probabilities among the variables should be estimated from the data.   Bushra's Response► Shruti's Video► Aras's Video►

Question 3: Write an SQL code to calculate the probability of negative outcome in the situation where the patient is severely ill and has not signed a "Do Not Resuscitate" (DNR) order.  Note that probabilities for events that are mutually exclusive and exhaustive should add up to one. Data► Bushra's Response►Anto's Video► Slides► SQL► 

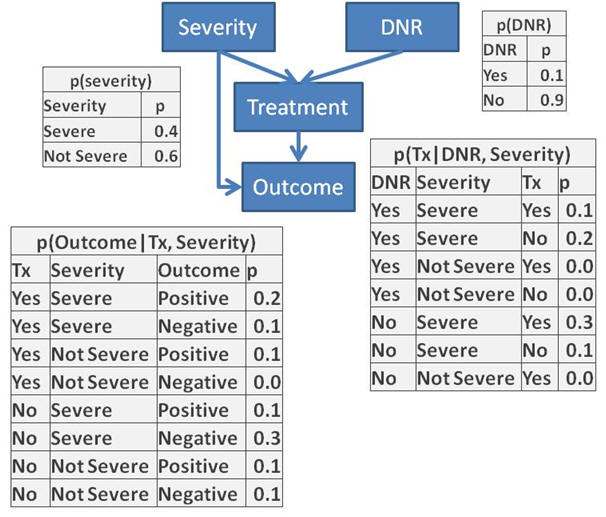
Question 4: Redo problem 3 in Netica or other software and verify the accuracy of your answer.  To accomplish this project organize the 4 node network inside Netica and direct the links between the nodes as in the graph structure.  Then for every node, enter the table of probabilities as per tables given in Question 3.  For example, for the DNR node enter the two probabilities of 0.1 and 0.9 into the Table within the node for DNR.  Once the entire network (the graph and the related probabilities) has been entered into Netica, evaluate the risks for a patient who is severely ill and has not signed a "Do Not Resuscitate" order.     Netica► Shruti's Video►

Question 5: Inside an electronic health record, there are data on outcomes of a particular intervention.  Using the network drawn below, write the equations that would allow you to estimate what would happen if the intervention was not given.  First, write an equation for each node in the network based on variables that precede it.  For example, the regression equation for predicting whether there is an adverse event is given by the equation:

 Outcome = a + b Treatment + c Severity

Second, set the variables that change across these equations to the relevant values.  For example, set Treatment to be zero. 

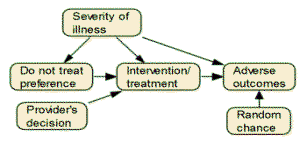
Question 6: The following graph was used to simulate data on bundling payment for total hip fracture treatment:

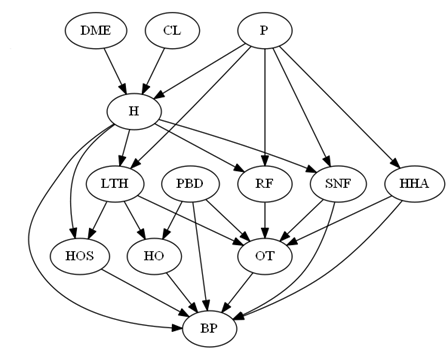
• Recover the original network and calculate the causal impact of H on BP.  Data► R Code► Detailed R Code►

• If you were using logistic or ordinary regression equations, write what set of equations are represented by the above network.  In each instance write all the variables that are in the regression equation and the variables that have a statistically significant relationship with the response variable.  For example, LTH is regressed on all variables that precede it which are DME, CL, P and H.  But only P and H have a statistically significant relationship with LTH.  This regression can be shown as:
  
  LTH = a + b DME + c CL + d P* + e H*
  
  In the above equation, the statistically significant relationships are shown with a star (*).  A missing star indicates an insignificant relation.  Using the data, estimates the parameters of each of the regressions.  Can these set of equations be used to create the network.  In how many ways does the regression equations differ from the network model in the graph. 

Question 7: Construct a decision aid for selection among antidepressants.   

1. Read about the STAR*D study protocol. Review►
2. Download data.  Use instructor's last name as password.  Data►
3. Repeat the following analysis for at least 5 antidepressant(s).  Separate analysis must be done for each antidepressant or antidepressant combination (shown in variable CONCAT). 
   • Create data sets for each antidepressant(s) combination.  This data sets will include a patient several times, if the patient received different combinations of antidepressants over time.  Group By Concat and ID variable to remove the weekly data. If the patient received the antidepressant(s) combination, assign it a value of 1 and otherwise, when they received other combination of antidepressant(s) assign it a value of 0.
   • Identify the parents in the Markov Blanket of each antidepressant.  You can use logistic regression to do this.  For each antidepressant use all variables that precede it as independent variables in the regression.  Use the variables that are significant predictors of the antidepressant as the parents in the Markov Blanket of the antidepressant. 
   • Stratify treatment and exclude from the list of parents in the Markov Blanket any variable not related to remission (measured as referred to follow-up).  Calculate the unconfounded impact of antidepressant(s) on remission.  Stratify the remaining variables in the parents in the Markov Blanket of treatment and calculate the impact of antidepressant(s) on remission.
4. Evaluate for a patient with PTSD and neurological disorders which of the 5 antidepressant(s) combination is most likely to lead to remission. 

More

For additional information (not part of the required reading), please see the following links:

1. Meta analysis through Bayesian networks Read►
2. Introduction to Bayesian networks Read►
3. Learning Bayesian Networks Read►
4. Selection of Judea Pearl's articles PubMed►
5. Applications of Bayesian networks in healthcare PubMed►
6. Use of graphs in removing confounding Read►
7. Learning Bayesian networks from correlated data Read►
8. Bayesian networks in neuroscience Read►
9. Cost analysis using Bayesian networks Read►
10. Comparison of Bayesian network and logistic models Read►
11. Bayesian network classifiers Read►
12. Introduction to Markov process Tim's Lecture►
13. Explanation of predictions Aloudah's Lecture►
14. Outcome based prescribing for citalopram Slides►