Assigned Reading
- Session Overview
- Network Concept
Assignment
Include in the first page a summary page. In the summary page
write statements comparing your work to answers given or videos. For
example, "I got the same answers as the Teach One video for question 1."
For these assignment you can use any statistical package, including R,
SAS, and SPSS, Python. R packages and BNLearn are also used often. OpenBUGS and
Gibbs Sampler, Stan, OpenMarkov, and Direct Graphical Model are also open
source software. Netica is free for networks less than 15 nodes.
Question 1: Draw networks based on the following independence assumptions.
When directed networks are possible, give formulas for predicting the last variable in the networks from marginal and pair-wise conditional probabilities. Keep in mind that absence of
independence assumption implies dependence.
Resources for Question 1:
| Nodes in Network |
Assumption |
| X, Y,
Z |
I(X,Y) |
| X, Y,
Z |
I(X,Y), Not I(X,Y|Z) |
| X, Y,
Z |
I(X,Y), I(X,Y|Z), Y
measured last |
| X, Y,
Z, W |
I(X,Y), I(X,Y|Z),
I({X,Y},W|Z), W measured last |
| X, Y,
Z, W |
II(X,Y), I(Z,W), and
X measured before Z and Y measured before W |
Question 2: Write an SQL code to calculate the probability of negative outcome in the situation
where the patient is severely ill and has not signed a "Do Not
Resuscitate" (DNR) order. Note that probabilities for
events that are mutually exclusive and exhaustive should add up to
one.
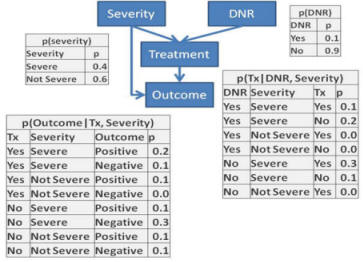
Additional resources for Question 2:
Question 3: Redo problem 2 in Netica or other software and verify the accuracy of your answer.
To accomplish this, organize the 4-node network inside Netica and direct the links between the nodes, as in the graph structure in question 3.
Then for every node, enter the table of probabilities as per tables given in Question 3. For example, for the DNR node enter the
two probabilities of 0.1 and 0.9 into the Table within the node for DNR. Once the entire network (the graph and the related
probabilities) has been entered into Netica, evaluate the risks for a patient who is severely ill and has not signed a "Do Not
Resuscitate" order.
Resources for Question 3:
Question 4: Throughout this course we emphasize the
concept of Markov blanket. A Markov blanket refers to a set of variables
that would make all other variables irrelevant in predicting the response
variable.
- If X1 and X2 are significant predictors of Y, X3
and X4 are not, and no interactions are significant; then what is the
Markov Blanket for Y? How is the concept of Markov Blanket related
to multi-colinearity?
- Suppose X2 occurs after Y and X1 occurs prior to Y, what is a Markov
Blanket that separates variables that are irrelevant and could possibly be
causes of Y. Keep in mind that a cause is something that occurs
prior to effect, has a significant association with the effect, has a
mechanism leading from cause to effect, and if cause is removed then the
effect is less likely to occur, Cetris Peribus.
Resources for Question 4:
Question 5: The following network shows the relationship between
symptoms of COVID and its diagnosis (shown as positive test result).
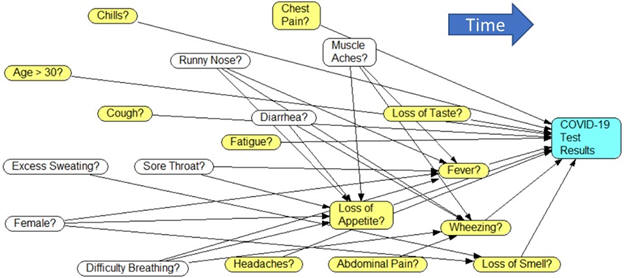
- What symptoms of COVID are neurological? What does ChatGPT say are
neurological symptoms of COVID?
- What symptoms of COVID are gastrointestinal in nature? What
symptoms are inflammatory? What are respiratory symptoms of COVID?
PubMed Review►
- Are all of the variables in the network correlated with each other?
- Does knowing that a female patient has a positive test result
increase the chance that she is over 30 years old?
- Is it correct to say that patients with cough and fever are likely
to have an elevated chance of positive COVID test?
- List the 5 symptoms of COVID that appear latest in progression of
the disease.
- Is muscle ache associated with positive COVID test result?
- Is throwing up associated with positive COVID test results?
- What is the Markov Blanket of fever?
- Under what condition is fever associated with chest pain?
- What are the co-parents of fever?
- Is muscle ache cause of fever or the reverse?
- Is sore throat a common cause or a common effect?
- If a patient does not currently have fever, what factors can be
used to establish whether the patient will develop fever later?
- What are the backdoor path from COVID test results to loss of
smell?
- Is runny nose associated with wheezing? with sore throat?
- Does presentation of COVID depend on the age of the patient?
- What variables are indirect predictors of COVID?
- What is the symptom most involved in mediating impact of indirect
variables on COVID test results?
- How many variables are direct predictors of COVID test results?
- Use ChatGPT to identify 10 alternative ways of indicating sore
throat? Can a language model be used to predict positive COVID test
results?
- Write an equation for calculating probability of fever from
patient's age, gender and presentation.
- Write an equation for calculating probability of excessive
sweating from patient's age, gender, and presentation
- If the patient reports some symptoms but not others should we
assume that symptoms not mentioned are not present?
Resources for answering Question 5:
- See Exhibit 20.1 for definition of various terms in Big Data in
Health Care, Chapter 20, page 492
More
For additional information (not part of the required reading), please see the following links:
- Introduction to causal inference
Read 1►
Read 2►
Video►
Slides►
- Meta analysis through Bayesian networks
Read►
- Introduction to Bayesian networks
Read►
- Learning Bayesian Networks
Read►
- Selection of Judea Pearl's articles
PubMed►
- Applications of Bayesian networks in healthcare PubMed►
- Use of graphs in removing confounding Read►
- Bayesian networks in neuroscience Read►
- Cost analysis using Bayesian networks Read►
- Bayesian network classifiers
Read►
- Introduction to Markov process
Tim's Lecture►
- Explanation of predictions Aloudah's Lecture►
This page is part of the course on Comparative Effectiveness by Farrokh Alemi, Ph.D.
Course Home►
Email►
|

