Assigned Reading
- Association networks
- Read chapter 19 in Statistical Analysis of Electronic Health
Records by Farrokh Alemi, 2020
- Statistical test of independence in 2 variables Slides►
- Statistical test of independence in 3 variables Slides►
- Independence test through Poisson regression
Slides►
- Jee Vang's lecture on independence test through Mutual Information Slides►
Assignment
Submit one file for all questions. Include all charts, code,
and output in the same file. Start each question in a separate
page or sheet. Include in the first page a summary page. In the
summary page write statements comparing your work to answers given or
videos. For example, "I got the same answers as the Teach One
video for question 1."
Question 1:
For this assignment you can use any statistical package including SQL or Excel. Work can be done in group's of two students but you cannot
work with a student that you have previously teamed up with.
A. For the following data:
|
MD |
RN |
Complaint |
Observed |
|
George |
Jim |
Yes |
53 |
|
George |
Jim |
No |
424 |
|
George |
Jill |
Yes |
11 |
|
George |
Jill |
No |
37 |
|
Smith |
Jim |
Yes |
0 |
|
Smith |
Jim |
No |
16 |
|
Smith |
Jill |
Yes |
4 |
|
Smith |
Jill |
No |
139 |
- Estimate chi-square for complete independence, 3 joint independence models,
and 3 homogenous models
- Which model best fits the data and why?
Shruti's response►
Aryan & Saeed's SQL►
Pearl's Teach One►
Pham's Teach One►
Question 2: In the following data, test which pair of variables
are independent and which pairs are associated. First calculate
the goodness of fit of a homogenous model (all main effects and all
pair wise associations). Then progressively remove one of the pairs from the
model until you can find a set of associations that fit the data.
R code►
Slides►
Hassan Abidi's Teach One►
Center for Medicare Services reimburses hip fracture treatment based on
one price for the hospital, physician or post acute care. Each
group continues to bill for their service as usual but at end of the
year the hospitals that have above average bundled costs are penalized
and hospitals that have below average bundled costs receive a financial
incentive. The hospital manager is interested to understand which
component of the operations contributes most to above average cost. The
data shows the number of hip fracture patients with above and below
average cost when cared for by various teams of clinicians. There
are five dimensions in the contingency table: orthopedic surgeon
(O), use of rehabilitation services (R), use of one of two skilled
nursing facilities (N), severity of patients' illness (S), and whether
the cost of the patient exceeded average bundled cost (A). You are
asked to fit a model that includes all pair-wise interactions, including
OR, ON, OS, OA, RN, RS, RA, NS, NA, and SA. Calculate the fit of
the model to the data using chi-square. Then remove one of the
pair-wise terms to see if it affects model performance significantly.
Continue to do so until you obtain a parsimonious model that describes
the relationships in the data and whose fit to the data cannot be
rejected. Verify that the associations shown in the
following Figure fits the result of your analysis. For every
associated pair in the model (significant or not significant), there
should be a link in the Figure. Identify which arc should not be
there and which arc should be there but is not there.
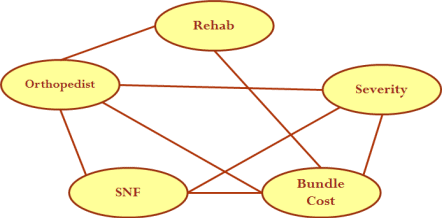
|
|
N: Skilled Nursing
Facility A |
Skilled Nursing Facility B |
|
S: High Severity |
Low
Severity |
High
Severity |
Low
Severity |
|
O: Orthopedic Surgeon |
R: Rehab Services |
A: > Bundle Cost |
< Bundle Cost |
> Bundle Cost |
< Bundle Cost |
> Bundle Cost |
< Bundle Cost |
> Bundle Cost |
< Bundle Cost |
| Joe |
Yes |
405 |
268 |
453 |
228 |
23 |
23 |
30 |
19 |
| Joe |
No |
13 |
218 |
28 |
201 |
2 |
19 |
1 |
18 |
| Jim |
Yes |
1 |
17 |
1 |
17 |
0 |
1 |
1 |
8 |
| Jim |
No |
1 |
117 |
1 |
133 |
0 |
12 |
0 |
17 |
|
Data adapted from Agresti A. Categorical Data Analysis, 3rd Edition, Wiley InterScience,
2013, page 381 |
Question 3. Select 3 variables from the STAR*D data and analyze the
independence relationship among the variables.
- Read about the STAR*D study protocol. Protocol►
- Download data. Use instructor's last name as password. Data 2010►
Data 2003►
- Select 3 variables
- Test 1 complete independence, 3 joint independence, and 3 homogenous associations.
- Identify the most parsimonious model whose fit to the data cannot be rejected
- Describe the meaning of your insight.
Arpitha and Shruti's Response►
Sheri Moinamin's
Teach One►
R Code►
Data►
More
For additional information (not part of the required reading), please see the following links:
- Introduction to chi-square test Read►
- Independence and Bayesian networks Video►
- Introduction to probability models Read► Slide►
- Event time stratification Read►
- Bayes rule & independence
Video►
- Estimating effects of nursing in clinical teams Read►
- Breaking nominal variables into binary variables Read►
- The relationship between chi-square statistics from matched and unmatched analyses Read►
- Jeff Lin's analysis of independence of 3 variables Read►
- Decomposable (independent) sub-graphs in 5 variable models
Read►
- Visualizing conditional probability
See►
This page is part of the course on Comparative Effectiveness Home► Email►
|
