Supplement to Chapter on Association Networks

Presentations

1. Association networks Read►
2. Introduction to chi-square test Read►
3. Statistical test of independence in 2 variables Slides►
4. Statistical test of independence in 3 variables Slides►
5. Independence test through Poisson regression Slides►
6. Jee Vang's lecture on independence test through Mutual Information Slides►

Assignment

Question 1: For this assignment you can use any statistical package including SQL or Excel.  Work can be done in group's of two students but you cannot work with a student that you have previously teamed up with.

A. For the following data:

1. Estimate chi-square for complete independence, 3 joint independence models, and 3 homogenous models
2. Which model best fits the data and why?  Shruti's response► Aryan & Saeed's SQL►

Question 2: In the following data, test which pair of variables are independent and which pairs are associated.  First calculate the goodness of fit of a homogenous model (all main effects and all pair wise associations).  Then progressively remove one of the pairs from the model until you can find a set of associations that fit the data. R code► Slides►

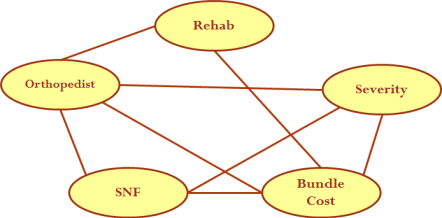
Center for Medicare Services reimburses hip fracture treatment based on one price for the hospital, physician or post acute care.  Each group continues to bill for their service as usual but at end of the year the hospitals that have above average bundled costs are penalized and hospitals that have below average bundled costs receive a financial incentive.  The hospital manager is interested to understand which component of the operations contributes most to above average cost. The data shows the number of hip fracture patients with above and below average cost when cared for by various teams of clinicians.  There are five dimensions in the contingency table:  orthopedic surgeon (O),  use of rehabilitation services (R), use of one of two skilled nursing facilities (N), severity of patients' illness (S), and whether the cost of the patient exceeded average bundled cost (A).  You are asked to fit a model that includes all pair-wise interactions, including OR, ON, OS, OA, RN, RS, RA, NS, NA, and SA.  Calculate the fit of the model to the data using chi-square.  Then remove one of the pair-wise terms to see if it affects model performance significantly.  Continue to do so until you obtain a parsimonious model that describes the relationships in the data and whose fit to the data cannot be rejected. Verify that the associations shown in the following Figure fits the result of your analysis.  For every associated pair in the model (significant or not significant), there should be a link in the Figure.  Identify which arc should not be there and which arc should be there but is not there. 

Question 3. Select 3 variables from the STAR*D data and analyze the independence relationship among the variables.

1. Read about the STAR*D study protocol. Protocol►
2. Download data.  Use instructor's last name as password.  Must enter password twice. Data 2010►  Data 2003►
3. Select 3 variables
4. Test 1 complete independence, 3 joint independence, and 3 homogenous associations.
5. Identify the most parsimonious model whose fit to the data cannot be rejected
6. Describe the meaning of your insight.

Arpitha and Shruti's Response► Sheri Moinamin's Teach One Video► R Code► Data►

More

For additional information (not part of the required reading), please see the following links:

1. Independence and Bayesian networks Video►
2. Introduction to probability models Read► Slide►
3. Event time stratification Read►
4. Bayes rule & independence Video►
5. Estimating effects of nursing in clinical teams Read►
6. Breaking nominal variables into binary variables Read►
7. The relationship between chi-square statistics from matched and unmatched analyses Read►
8. Jeff Lin's analysis of independence of 3 variables Read►
9. Decomposable (independent) sub-graphs in 5 variable models Read►
10. Visualizing conditional probability See►