Lecture: Causal Networks of Regressions
Assigned Reading
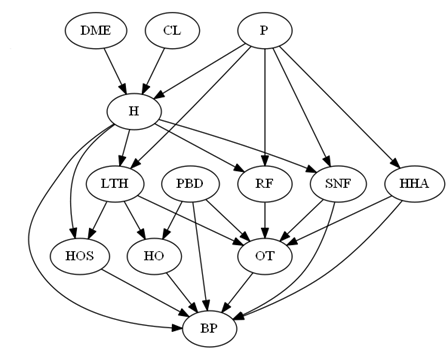
AssignmentInclude in the first page a summary page. In the summary page write statements comparing your work to answers given or videos. For example, "I got the same answers as the Teach One video for question 1." Question 1: This lecture shows how regressions can be used to identify a network structure. The basic idea is that one regress a response variable (one of the nodes in the network) on all variables that precede it. Thus, the independent variables are all preceding variables. The statistically significant variables (in case of LASSO regression, the non-zero variables) in the regressions indicate the parents in the Markov Blanket of the variable. And the collection of all parents in Markov Blanket identify the entire network structure. Write out the set of equations that can identify the following network:
In each instance write all the variables that are in the regression equation. These include the response (dependent) and the independent variable. Mark with * the independent variables that have a statistically significant (non-zero) relationship with the response variable. For example, LTH is regressed on all variables that precede it which are DME, CL, P and H. But only P and H have a statistically significant relationship with LTH. This regression can be shown as: LTH = a + b DME + c CL + d P* + e H* Resources for Question 1: Question 2: Construct a Bayesian probability network model that would
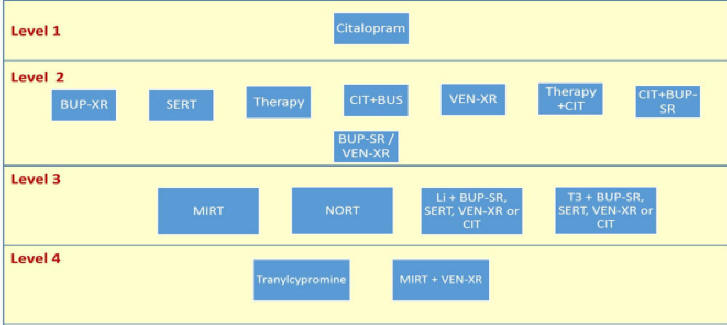
predict success with antidepressants. A network model will include
variables, and mediators of the effect of variables, on response to
the antidepressant. Include all baseline diagnoses and gender as
covariates. Assume that gender occurs before baseline
diagnoses. Baseline diagnoses occur before any treatment. Assume that antidepressant treatments occur
before report of remission and in the
following order: Remission should be considered an end node. Gender is a
root node. All other variables, e.g. diagnoses, could be either
root or intermediary nodes but all occur prior to use of
antidepressant. The antidepressants that were given prior to an
antidepressant should be used as a covariate. The data has been
modified to report per person data, without visit-based weekly data.
Resources for Question 2:
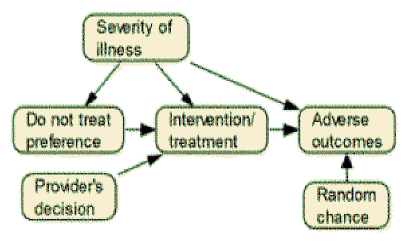
Question 3: Inside an electronic health record, there are data on outcomes of a particular intervention. Using the network drawn below, write the equations that would allow you to estimate what would happen if the intervention was not given. First, write an equation for each node in the network based on that variables that precede it and indicate the significant relations with an astric.
Resources for Question 3:
Question 4: The following graph was used to simulate data on bundling payment for total hip fracture
treatment.
Recover the original network from the data using LASSO regression and
calculate the causal impact of H on BP using Netica. Resources for Question 4:
Question 5: This problem focuses on temporal analysis of the variables. This problem was adapted from “Langville AN, Meyer CD. The Science of Rating and Ranking Who’s Number 1. Princeton University Press, 2012“. The following data show for how many people one disease occurs before another. To judge which disease occurs first, we focus on patients who had both disease. Patients who had one but not the other disease do not count in these calculations. For example, in patients who had both "D" and "M", for 7 patients "D" occurred before "M"; and for 52 patients "M" occurred before "D". For patients who had both "N" and "U", N occurs before U for 7 patients; and the reverse occurs for 5 patients.
Resources for Question 5: Question 6: The following data show for how many patients one disease occurs before another. For example, for 21 patients D occurs before N and for 24 patients the reverse order occurs. There is no patient in our sample where both U and M have occurred in the same person. Which of the following statements are correct, if we consider the relationship between these two diseases and the rest of the diseases?
Resources for Question 6: Question 7:
Draw a network that explains
variation in Y from its direct, and indirect, causes.
Draw the network based on the following 5 regressions.
Statistically significant variables are indicated by a
circle 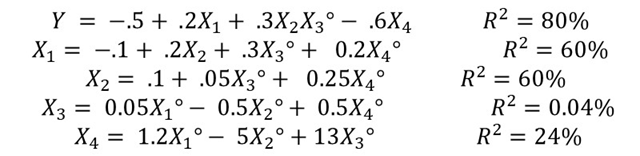
Resources available for this question
MoreFor additional information (not part of the required reading), please see the following links:
This page is part of the course on Causal Analysis by Farrokh Alemi, Ph.D. Course Home► Email► |